Cách Sử Dụng Máy Tính Để Tính Đạo Hàm Chính Xác Nhất

Việc thành thạo cách sử dụng máy tính để tính đạo hàm là một kỹ năng thiết yếu đối với học sinh, sinh viên và các chuyên gia trong nhiều lĩnh vực. Đạo hàm, một khái niệm cơ bản của giải tích, đóng vai trò quan trọng trong việc phân tích sự biến thiên và tốc độ thay đổi của các hàm số. Với sự hỗ trợ của các loại máy tính Casio hay Vinacal hiện đại, người dùng có thể nhanh chóng và chính xác tìm ra đạo hàm của những hàm số phức tạp, từ đó tối ưu hóa bài toán và đẩy mạnh ứng dụng thực tiễn trong khoa học kỹ thuật. Bài viết này sẽ cung cấp hướng dẫn chi tiết về cách thực hiện phép tính đạo hàm trên máy tính, giúp bạn nắm vững công cụ mạnh mẽ này.

Đạo Hàm Là Gì? Khái Niệm Và Ý Nghĩa Sâu Sắc Trong Toán Học

Trong lĩnh vực giải tích toán học, đạo hàm là một khái niệm cốt lõi biểu thị sự biến thiên của một hàm số tại một điểm cụ thể. Nó là tỷ lệ thay đổi tức thời của hàm số so với đối số tại điểm đó. Độ lớn và hướng của sự biến thiên này đại diện cho giá trị của đạo hàm. Hiểu đơn giản, đạo hàm cho biết hàm số đang tăng hay giảm và tăng giảm nhanh đến mức nào.

Công thức chung để tính đạo hàm của hàm số y=f(x) tại điểm x0 được định nghĩa như sau: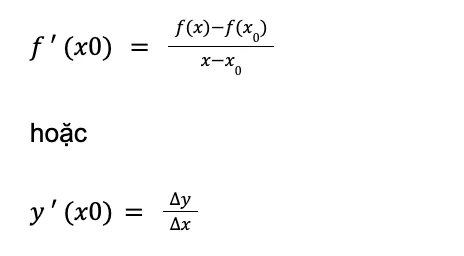

Công thức tính đạo hàm cơ bản hiển thị trên màn hình, giải thích cách sử dụng máy tính để tính đạo hàm

Trong công thức này, Δx là sự thay đổi cực nhỏ của đối số x, và Δy là sự thay đổi tương ứng của hàm số y. Giới hạn khi Δx tiến về 0 chính là giá trị đạo hàm. Công thức này là nền tảng cho mọi phép tính đạo hàm sau này.

Ý nghĩa của đạo hàm được thể hiện rõ ràng qua hai khía cạnh chính. Thứ nhất là khía cạnh hình học, nơi đạo hàm tại một điểm x0 của hàm số f(x) chính là hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm (x0, f(x0)). Nó mô tả độ dốc của đường cong tại điểm đó.

Thứ hai là khía cạnh vật lý, trong đó đạo hàm thường được hiểu là vận tốc tức thời của một vật chuyển động. Nếu hàm số f(t) biểu diễn vị trí của vật theo thời gian t, thì f'(t) chính là vận tốc tức thời của vật tại thời điểm t. Đạo hàm cấp hai sẽ biểu thị gia tốc.

Tầm quan trọng của đạo hàm còn lan rộng ra nhiều ngành khoa học khác. Trong kinh tế, nó giúp phân tích tốc độ thay đổi của chi phí, doanh thu. Trong kỹ thuật, đạo hàm dùng để thiết kế hệ thống điều khiển, phân tích tín hiệu. Nắm vững khái niệm đạo hàm là chìa khóa để giải quyết nhiều bài toán phức tạp.

Hướng Dẫn Chi Tiết Cách Sử Dụng Máy Tính Để Tính Đạo Hàm

Việc tính toán đạo hàm bằng máy tính giúp tiết kiệm thời gian và giảm thiểu sai sót. Để thực hiện cách sử dụng máy tính để tính đạo hàm, bạn cần chọn một loại máy tính khoa học có tích hợp chức năng đạo hàm hoặc phần mềm tính toán chuyên dụng. Dưới đây là hướng dẫn chi tiết cho một số dòng máy phổ biến.

Cách Tính Đạo Hàm Với Máy Tính Casio FX-580VN

Máy tính Casio FX-580VN là một công cụ quen thuộc và mạnh mẽ, được sử dụng rộng rãi. Dòng máy này cung cấp chức năng tính đạo hàm một cách trực tiếp, giúp người dùng nhanh chóng có được kết quả. Việc sử dụng thành thạo máy Casio FX-580VN sẽ hỗ trợ rất nhiều trong học tập và công việc.

Quy trình tính đạo hàm cấp 1

Để tính đạo hàm cấp 1 của một hàm số tại một điểm trên Casio FX-580VN, bạn thực hiện theo các bước sau. Đây là phương pháp cơ bản nhất mà bạn cần nắm vững.

Bước 1: Kích hoạt chức năng đạo hàm. Nhấn tổ hợp phím SHIFT và sau đó là nút tích phân (∫dx). Màn hình máy tính sẽ hiển thị ký hiệu d/dx.

Bước 2: Nhập biểu thức hàm số cần tìm đạo hàm vào ô vuông lớn đầu tiên. Sử dụng các phím số và phép toán để nhập chính xác hàm f(x). Đảm bảo rằng hàm số được nhập đúng cú pháp.

Bước 3: Nhập giá trị x cụ thể vào ô vuông nhỏ bên dưới. Đây là điểm mà bạn muốn tính đạo hàm của hàm số. Sau khi nhập xong, nhấn phím = để máy tính thực hiện phép tính.

Hướng dẫn cách sử dụng máy tính Casio FX-580VN để tính đạo hàm cấp 1

Kết quả hiển thị trên màn hình chính là giá trị đạo hàm cấp 1 của hàm số tại điểm x đã nhập. Quá trình này rất nhanh chóng và tiện lợi cho việc kiểm tra kết quả.

Quy trình tính đạo hàm cấp 2

Việc tính đạo hàm cấp 2 trên Casio FX-580VN đòi hỏi một chút thủ thuật, vì máy không có chức năng đạo hàm cấp 2 trực tiếp. Chúng ta sẽ áp dụng phương pháp xấp xỉ bằng cách sử dụng đạo hàm cấp 1 hai lần. Đây là một cách thông minh để mở rộng khả năng của máy.

Bước 1: Tính đạo hàm cấp 1 của hàm số tại điểm x = x0. Bạn cần áp dụng các bước đã hướng dẫn ở trên để có được f'(x0). Ghi nhớ hoặc lưu giá trị này.

Bước 2: Tính đạo hàm cấp 1 của hàm số tại điểm x = x0 + ε, với ε là một giá trị rất nhỏ (ví dụ: 0,000001). Đây là f'(x0 + ε). Lưu giá trị này vào bộ nhớ của máy tính (ví dụ biến A).

Bước 3: Sử dụng công thức xấp xỉ đạo hàm cấp 2: f”(x0) ≈ (f'(x0 + ε) – f'(x0)) / ε. Nhập công thức (Ans – PreAns)/ε vào máy tính và nhấn phím =. Trong đó Ans là kết quả f'(x0 + ε) và PreAns là kết quả f'(x0) đã lưu.

Kết quả thu được sẽ là giá trị xấp xỉ của đạo hàm cấp 2 tại x0. Phương pháp này yêu cầu sự cẩn thận trong việc nhập giá trị và ghi nhớ các bước.

Cách Tính Đạo Hàm Với Máy Tính Casio FX-880BTG

Máy tính Casio FX-880BTG là dòng máy tính khoa học hiện đại hơn, với giao diện trực quan và nhiều tính năng cải tiến. Chức năng tính đạo hàm (Derivative – d/dx) trên Casio 880 được tích hợp trong danh mục Func Analysis, dễ dàng truy cập từ mục CATALOG. Điều này giúp việc sử dụng máy tính để tính đạo hàm trở nên thuận tiện hơn.

Để truy cập tính năng Derivative, bạn vào mục CATALOG, tìm đến Func Analysis và chọn d/dx. Tính năng này cho phép bạn tính toán đạo hàm tại một điểm cụ thể, tương tự như các dòng máy Casio khác.

Cú pháp nhập đạo hàm trên Casio FX-880BTG có thể thay đổi tùy thuộc vào cài đặt Input/Output trên menu SETTINGS. Điều này ảnh hưởng đến cách bạn nhập biểu thức và điểm x. Hãy kiểm tra cài đặt của máy trước khi thực hiện.

Khi cài đặt Input/Output là MathI/MathO hoặc MathI/DecimalO, cú pháp nhập sẽ hiển thị một cách tự nhiên. Bạn sẽ thấy các ô trống để nhập hàm số và giá trị x một cách trực quan, giống như viết trên giấy.

Nếu cài đặt là LineI/LineO hoặc LineI/DecimalO, cú pháp sẽ là d/dx(biểu thức, x, giá trị). Bạn cần nhập hàm số, biến số x và giá trị x cần tính đạo hàm theo thứ tự này, phân tách bằng dấu phẩy.

Tính năng Derivative trên Casio FX-880BTG không chỉ hữu ích trong tính toán cơ bản mà còn mở rộng ứng dụng trong các chế độ khác như Calculate, Table, Vector, Ratio, Equation, Matrix và Spreadsheet. Điều này tăng cường khả năng phân tích toán học của người dùng.

Hướng Dẫn Chi Tiết Cách Sử Dụng Máy Tính Vinacal Để Tính Đạo Hàm

Máy tính Vinacal cũng là một lựa chọn phổ biến, đặc biệt trong môi trường học đường. Việc tính đạo hàm trên Vinacal cũng tương tự như Casio, với các bước rõ ràng và dễ thực hiện. Nắm vững cách sử dụng Vinacal là một lợi thế.

Để tính đạo hàm của một hàm số trên máy tính Vinacal, bạn sẽ sử dụng chức năng tính đạo hàm d/dx. Quy trình này khá đơn giản và trực quan.

Bước 1: Nhấn tổ hợp phím để kích hoạt chức năng đạo hàm. Thông thường, bạn sẽ nhấn SHIFT và nút tích phân (∫dx) để hiển thị ký hiệu d/dx trên màn hình.

Bước 2: Nhập hàm số f(x) vào phần biểu thức. Sau đó, nhập giá trị x tại điểm bạn muốn tính đạo hàm. Ví dụ, để tính đạo hàm tại x = 100, bạn nhập hàm và sau đó điền 100 vào vị trí x.

Thủ thuật “CALC X = 100” đôi khi được sử dụng để kiểm tra đạo hàm một cách gián tiếp. Bằng cách thay một giá trị x lớn và sau đó biểu diễn kết quả thông qua biến X, người dùng có thể suy luận ra dạng đạo hàm. Tuy nhiên, phương pháp này đòi hỏi kinh nghiệm và hiểu biết về cấu trúc của đạo hàm.

Cách Sử Dụng Máy Tính Để Tính Đạo Hàm Của Hàm Logarit Và Hàm Số Mũ

Hàm logarit và hàm số mũ là những dạng hàm số thường gặp trong toán học và khoa học. Việc tính đạo hàm của chúng bằng máy tính cũng tuân theo quy trình tương tự như các hàm số khác. Tuy nhiên, cần lưu ý đến tập xác định và các quy tắc đặc biệt.

Công thức đạo hàm cơ bản cho hàm Logarit và hàm số mũ

Trước khi sử dụng máy tính, việc nắm vững các công thức đạo hàm cơ bản của hàm logarit và hàm số mũ là rất quan trọng. Ví dụ, đạo hàm của ln(x) là 1/x, và đạo hàm của e^x là e^x. Việc hiểu lý thuyết giúp bạn kiểm tra kết quả của máy tính.

Các bước bấm máy tính đạo hàm logarit hoặc hàm số mũ:

Bước 1: Chọn một giá trị x = x0 bất kỳ thuộc tập xác định của hàm số. Điều này đảm bảo rằng phép tính là hợp lệ và có ý nghĩa. Tránh các điểm biên hoặc điểm mà hàm số không xác định.

Bước 2: Sử dụng chức năng đạo hàm của máy tính (d/dx) để tính đạo hàm của hàm số y = f(x) tại điểm x = x0. Ghi lại kết quả hiển thị trên màn hình. Đây là giá trị đạo hàm số.

Bước 3: Nếu bạn đang làm bài toán trắc nghiệm, hãy thay giá trị x = x0 vào từng đáp án A, B, C, D. So sánh kết quả của từng đáp án với kết quả bạn vừa tính ở bước 2. Đáp án nào trùng khớp sẽ là đáp án chính xác.

Ví dụ, để tính đạo hàm của y = ln(2x) tại x = 1. Bạn nhập ln(2x) vào máy, đặt x = 1. Kết quả máy tính sẽ cho ra 1. Sau đó, bạn kiểm tra các đáp án trắc nghiệm bằng cách thay x = 1.

Các Trường Hợp Đặc Biệt Và Lưu Ý Khi Tính Đạo Hàm Bằng Máy Tính

Mặc dù máy tính là công cụ mạnh mẽ, nhưng vẫn có những giới hạn và trường hợp đặc biệt cần lưu ý khi tính đạo hàm. Việc hiểu rõ những điểm này giúp bạn tránh sai sót và sử dụng máy tính hiệu quả hơn.

Hàm số không xác định hoặc không khả vi tại điểm x0

Máy tính chỉ có thể tính đạo hàm tại một điểm nếu hàm số xác định và khả vi tại điểm đó. Nếu bạn cố gắng tính đạo hàm tại một điểm mà hàm số không xác định (ví dụ: chia cho 0) hoặc không khả vi (ví dụ: tại đỉnh nhọn của hàm trị tuyệt đối), máy tính có thể báo lỗi hoặc cho ra kết quả không chính xác. Luôn kiểm tra tập xác định và tính liên tục của hàm số.

Sai số làm tròn của máy tính

Máy tính thực hiện phép tính với độ chính xác hữu hạn, dẫn đến sai số làm tròn nhỏ. Khi tính đạo hàm, đặc biệt là đạo hàm cấp cao hoặc hàm số phức tạp, sai số này có thể tích lũy. Điều này thường không ảnh hưởng đến các bài toán cơ bản nhưng cần lưu ý trong các ứng dụng khoa học yêu cầu độ chính xác cực cao.

Giới hạn của máy tính: không tìm được biểu thức đạo hàm tổng quát

Một hạn chế lớn của máy tính cầm tay là chúng chỉ có thể tính giá trị đạo hàm tại một điểm cụ thể, chứ không thể tìm ra biểu thức đạo hàm tổng quát của hàm số. Ví dụ, máy tính có thể cho bạn biết đạo hàm của x^2 tại x=3 là 6, nhưng nó không thể cho bạn biết đạo hàm của x^2 là 2x. Đối với việc tìm biểu thức đạo hàm, bạn cần sử dụng kiến thức lý thuyết hoặc phần mềm toán học chuyên dụng (như Maple, Mathematica).

Kiểm tra kết quả bằng phương pháp thủ công hoặc online tool khác

Để tăng cường độ tin cậy của kết quả, bạn nên kiểm tra lại bằng cách tính đạo hàm thủ công (nếu có thể) hoặc sử dụng các công cụ tính đạo hàm trực tuyến khác. Việc này giúp bạn phát hiện lỗi nhập liệu hoặc hiểu sai về chức năng của máy tính. Đối chiếu kết quả là một bước quan trọng trong quá trình học và làm việc.

Tầm quan trọng của việc hiểu lý thuyết đạo hàm

Máy tính là công cụ hỗ trợ, không phải là thay thế cho kiến thức. Việc hiểu rõ định nghĩa, công thức và ý nghĩa của đạo hàm giúp bạn diễn giải kết quả của máy tính một cách chính xác. Nó cũng giúp bạn nhận biết khi nào kết quả máy tính có vẻ sai hoặc không hợp lý. Lý thuyết là nền tảng để sử dụng công cụ một cách thông minh.

Thủ Thuật Và Ví Dụ Thực Hành Nâng Cao Khi Tính Đạo Hàm

Để củng cố kỹ năng cách sử dụng máy tính để tính đạo hàm, chúng ta sẽ xem xét một số ví dụ thực hành cụ thể. Các ví dụ này sẽ giúp bạn áp dụng các bước đã học vào thực tế và hiểu rõ hơn về cách các dòng máy tính xử lý phép toán đạo hàm.

Ví dụ Tính Đạo Hàm Cấp 1

Cho hàm số y = √(4x – 1). Hãy tính đạo hàm của hàm số này tại x = 2.
Đây là một bài toán đạo hàm cơ bản, minh họa rõ ràng quy trình sử dụng máy tính.

Bước 1: Kích hoạt chức năng đạo hàm. Nhấn tổ hợp phím SHIFT + nút đạo hàm (∫dx) trên máy tính Casio. Màn hình sẽ hiển thị biểu tượng d/dx( ).

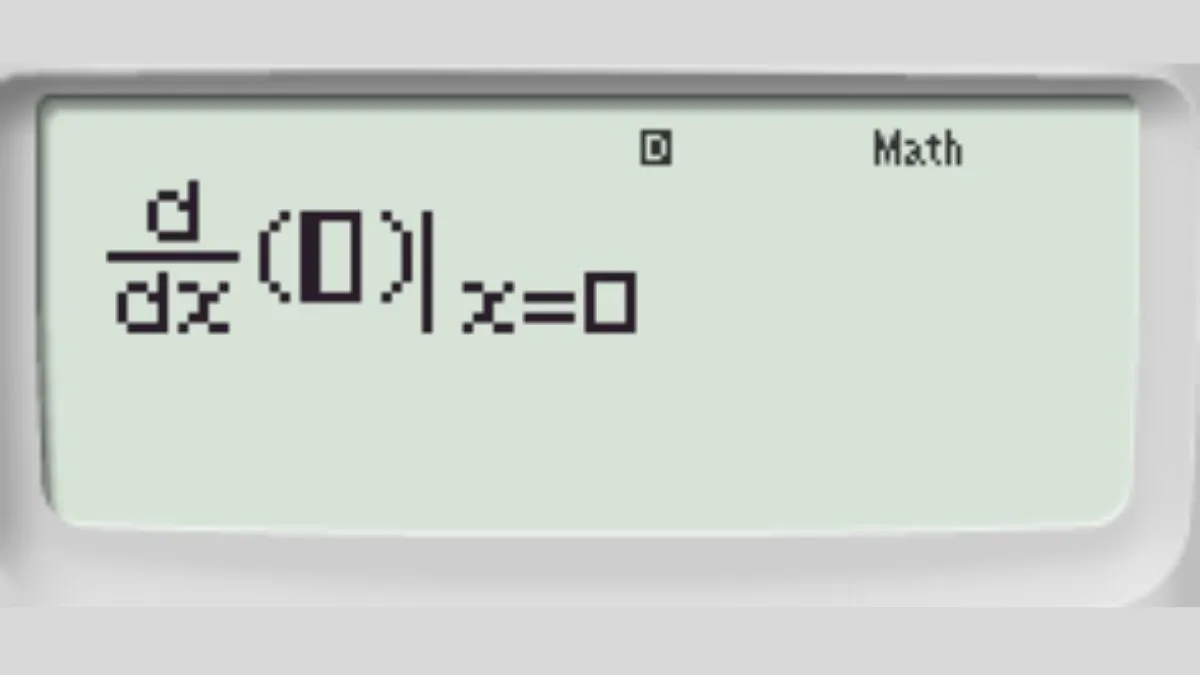Bàn phím máy tính Casio hiển thị bước đầu tiên để tính đạo hàm cấp 1 của một hàm số

Bước 2: Nhập hàm số và giá trị x. Nhập √(4x – 1) vào vị trí biểu thức và x = 2 vào vị trí điểm cần tính. Đảm bảo cú pháp chính xác.

Sau khi nhấn phím “=”, máy tính sẽ hiển thị kết quả.

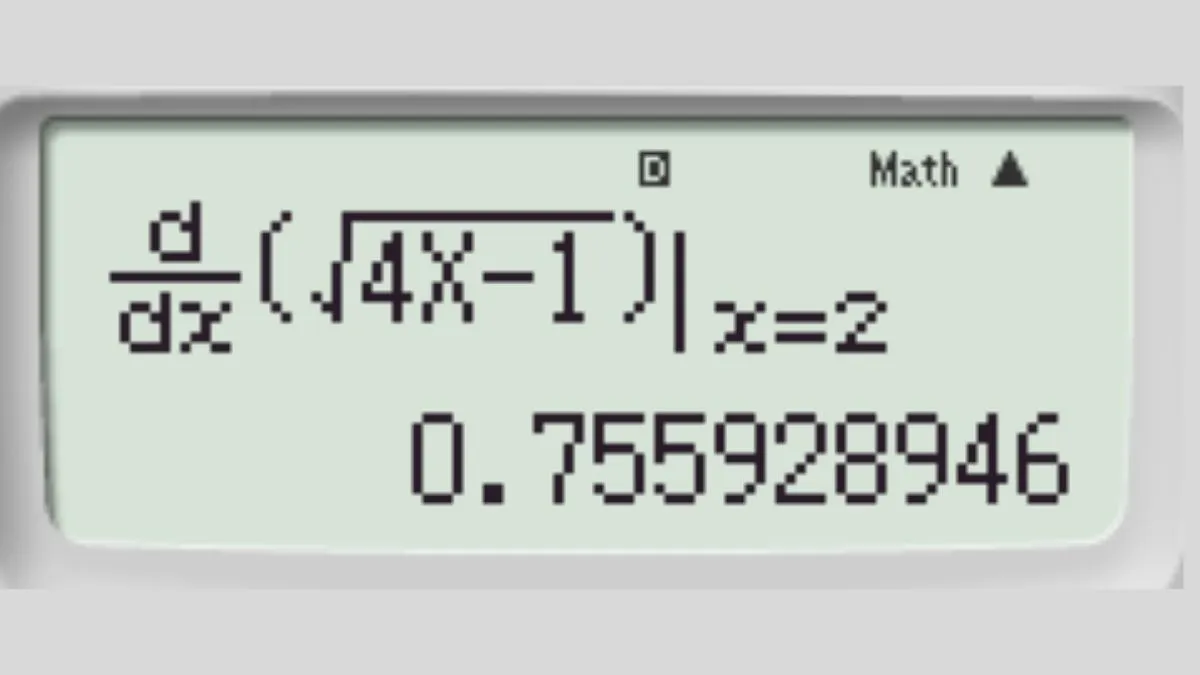Kết quả đạo hàm cấp 1 được tính bằng máy tính Casio, minh họa cách sử dụng máy tính để tính đạo hàm

Kết quả là 1. Đây là giá trị đạo hàm cấp 1 của hàm số tại x = 2.

Ví dụ Tính Đạo Hàm Cấp 2

Tính giá trị gần đúng đạo hàm cấp hai của hàm số f(x) = x^3 – 5x + 7 tại x0 = 3.
Bài toán này yêu cầu áp dụng phương pháp xấp xỉ đạo hàm cấp 2 đã được hướng dẫn.

Bước 1: Tính đạo hàm cấp 1 của hàm số tại x0 = 3. Nhập hàm số x^3 – 5x + 7 vào chức năng d/dx, và x = 3.

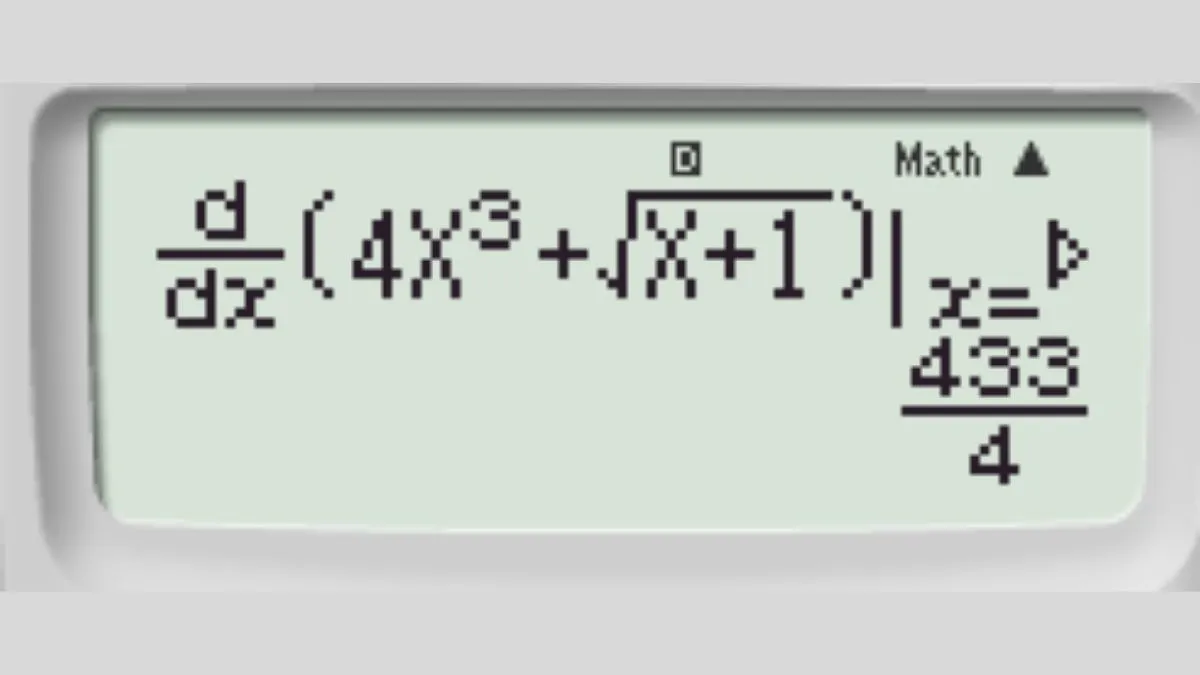Các bước tính đạo hàm cấp 2 trên máy tính Casio, hiển thị kết quả trung gian

Kết quả sẽ là 22.

Bước 2: Lưu kết quả vừa tìm được (22) vào một biến nhớ, ví dụ biến A. Nhấn SHIFT + STO + (-) (ký hiệu A). Giá trị 22 bây giờ được lưu trữ trong A.

Bước 3: Tính đạo hàm cấp 1 của hàm số tại x0 = 3 + 0.000001. Nhập hàm số và x = 3.000001 vào chức năng d/dx.

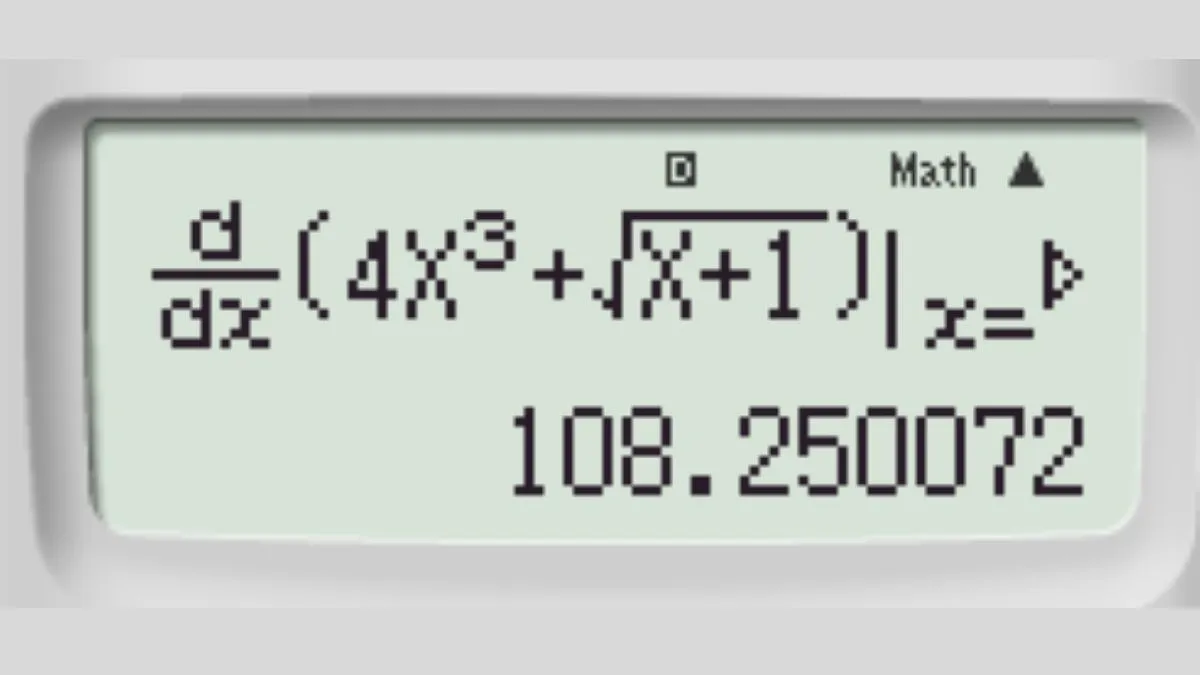Màn hình máy tính Casio hiển thị kết quả cuối cùng khi tính đạo hàm cấp 2

Kết quả sẽ là 22.000018. Lưu giá trị này vào một biến khác, ví dụ biến B. Nhấn SHIFT + STO + “` (ký hiệu B).

Bước 4: Tính (B – A) / 0.000001. Đây là công thức xấp xỉ đạo hàm cấp 2. Nhập vào máy tính (Ans – PreAns)/0.000001 hoặc (B – A)/0.000001.

Kết quả sẽ xấp xỉ 18. Đây chính là giá trị gần đúng của đạo hàm cấp 2 của hàm số f(x) tại x = 3.

Việc nắm vững cách sử dụng máy tính để tính đạo hàm là một kỹ năng vô cùng giá trị. Nó không chỉ giúp tăng tốc độ giải quyết bài toán mà còn nâng cao độ chính xác. Từ việc hiểu khái niệm cơ bản đến áp dụng trên các dòng máy Casio hay Vinacal, người dùng đều có thể hưởng lợi từ công cụ mạnh mẽ này. Thực hành thường xuyên với các ví dụ cụ thể sẽ giúp bạn thành thạo hơn, từ đó tiết kiệm thời gian và tập trung vào việc phân tích sâu hơn các khía cạnh toán học, khoa học hoặc kỹ thuật của bài toán.

Ngày Cập Nhật Mới Nhất: Tháng 10 24, 2025 by Cơ khí Quốc Cường